(本小题满分12分)
设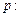 实数
实数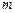 满足
满足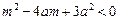 (其中
(其中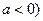 ;
;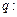 实数
实数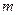 满足方程
满足方程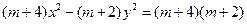 为双曲线.若
为双曲线.若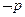 是
是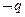 的必要不充分条件,求实数
的必要不充分条件,求实数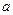 的取值范围.
的取值范围.
(本小题满分12分)
如图,正方体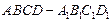 的棱长为
的棱长为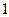 ,点
,点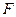 为
为 的中点.
的中点.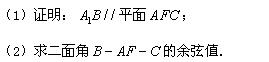
(本小题满分14分)
已知常数a为正实数,曲线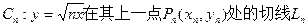 总经过定点(
总经过定点( ,0)
,0)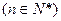
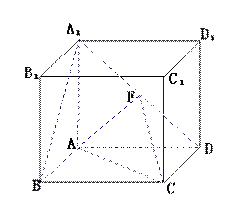
(1) 求证:点列: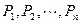 在同一直线上
在同一直线上
(2) 求证: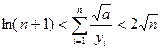
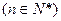
(本小题满分14分)
设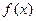 是定义在
是定义在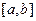 上的函数,用分点
上的函数,用分点
将区间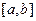 任意划分成
任意划分成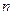 个小区间,如果存在一个常数
个小区间,如果存在一个常数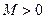 ,使得和式
,使得和式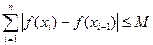 (
(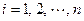 )恒成立,则称
)恒成立,则称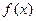 为
为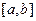 上的有界变差函数.
上的有界变差函数.
(1)函数 在
在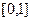 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数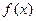 是
是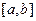 上的单调递减函数,证明:
上的单调递减函数,证明: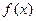 为
为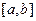 上的有界变差函数;
上的有界变差函数;
(3)若定义在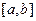 上的函数
上的函数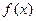 满足:存在常数
满足:存在常数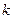 ,使得对于任意的
,使得对于任意的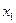 、
、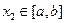 时,
时,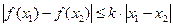 .证明:
.证明: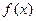 为
为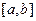 上的有界变差函数.
上的有界变差函数.
(本小题共14分)
已知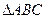 的边
的边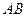 边所在直线的方程为
边所在直线的方程为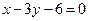
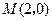 满足
满足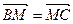 , 点
, 点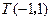 在AC边所在直线上
在AC边所在直线上
且满足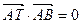 .
.
(I)求AC边所在直线的方程;
(II)求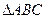 外接圆的方程;
外接圆的方程;
(III)若动圆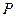 过点
过点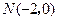 ,且与
,且与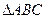 的外接圆外切,求动圆
的外接圆外切,求动圆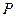 的圆心的轨迹方程.请注意下面两题用到求和符号:
的圆心的轨迹方程.请注意下面两题用到求和符号:
f(k)+f(k+1)+f(k+2)+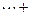 f(n)=
f(n)=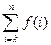 ,其中k, n为正整数且k
,其中k, n为正整数且k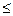 n
n