在 中,内角
中,内角 的对边分别为
的对边分别为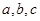 ,并且
,并且 .
.
(1)求角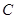 的大小;
的大小;
(2)若 ,求
,求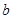 .
.
已知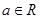 ,命题
,命题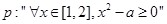 ,命题
,命题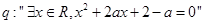 .
.
(Ⅰ)若命题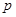 为真命题,求实数
为真命题,求实数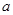 的取值范围;
的取值范围;
(Ⅱ)若命题 为假命题,求实数
为假命题,求实数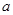 的取值范围.
的取值范围.
已知直线 为函数
为函数 的图像,曲线C为二次函数
的图像,曲线C为二次函数 的图像,直线
的图像,直线 与曲线C交于不同两点A,B
与曲线C交于不同两点A,B
(I)当 时,求弦AB的长;
时,求弦AB的长;
(II)求线段AB中点的轨迹方程;
(III)试利用抛物线的定义证明:曲线C为抛物线.
已知椭圆 的左焦点为
的左焦点为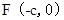 ,离心率为
,离心率为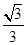 ,点M在椭圆上且位于第一象限,直线FM被圆
,点M在椭圆上且位于第一象限,直线FM被圆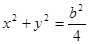 截得的线段的长为c,
截得的线段的长为c, .
.
(I)求直线FM的斜率;
(II)求椭圆的方程;
(III)设椭圆上动点P在x轴上方,若直线FP的斜率大于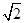 ,求直线OP(O为原点)的斜率的取值范围.
,求直线OP(O为原点)的斜率的取值范围.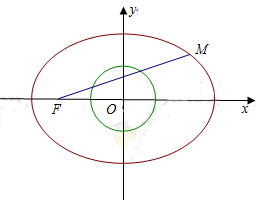
设椭圆E的方程为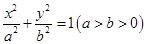 ,点O为坐标原点,点A的坐标为
,点O为坐标原点,点A的坐标为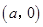 ,点B的坐标为
,点B的坐标为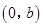 ,点M在线段AB上,满足
,点M在线段AB上,满足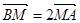 ,直线OM的斜率为
,直线OM的斜率为 .
.
(I)求E的离心率e;
(II)设点C的坐标为 ,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为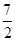 ,求E的方程.
,求E的方程.
在平面直角坐标系xOy中,椭圆C的参数方程 (φ为参数),直线
(φ为参数),直线 的参数方程
的参数方程 (t为参数) .
(t为参数) .
(I)求C与 的普通方程;
的普通方程;
(II)求过C的右焦点,且平行 的直线方程.
的直线方程.