将棱长为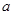 的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点
的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点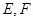 分别是
分别是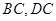 的中点.
的中点.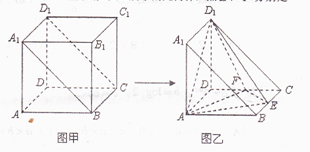
(Ⅰ)证明: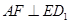 ;
;
(Ⅱ)求三棱锥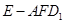 的体积.
的体积.
(本题12分)设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若 是从区间
是从区间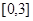 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(本题12分)椭圆C: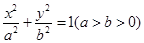 的两个焦点为F1,F2,点P在椭圆C上,且
的两个焦点为F1,F2,点P在椭圆C上,且 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于 两点,且A
两点,且A 、B关于点M对称,求直线l的方程.
、B关于点M对称,求直线l的方程.
(本题10分)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
(本小题满分12分) 过圆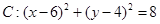 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于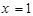 的对称点为E,关于
的对称点为E,关于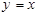 的对称点为F,求|EF|的取值范围.
的对称点为F,求|EF|的取值范围.
(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD为菱形,PD=AD,∠DAB="60°," PD⊥底面ABCD.
(1)求作平面PAD与平面PBC的交线,并加以证明;
(2)求PA与平面PBC所成角的正弦值;
(3) 求平面PAD与平面PBC所成锐二面角的正切值。
求平面PAD与平面PBC所成锐二面角的正切值。