设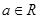 ,函数
,函数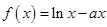 .
.
(1)若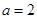 ,求曲线
,求曲线 在点
在点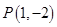 处的切线方程;
处的切线方程;
(2)若 无零点,求实数
无零点,求实数 的取值范围;
的取值范围;
(3)若 有两个相异零点
有两个相异零点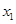 、
、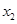 ,求证:
,求证: .
.
(本题满分10分) 选修4—5:不等式选讲
(1)解关于x的不等式 ;
;
(2)若关于 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围.
.(本题满分10分) 选修4—4:坐标系与参数方程
已知曲线C1的极坐标方程为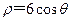 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ,曲线C1,C2相交于点A、B.
,曲线C1,C2相交于点A、B.
(1)分别将曲线C1,C2的极坐标方程化为直角坐标方程;
(2)求弦AB的长.
(本题满分10分)选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,切点为C,若PC=2 ,求PD的长.
,求PD的长.
(本题满分12分)已知椭圆 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点(4,0)且不与坐标轴垂直的直线 交椭圆
交椭圆 于
于 、
、 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 .求证:直线
.求证:直线 过
过 轴上的一定点,并求出此定点坐标.
轴上的一定点,并求出此定点坐标.
(本题满分12分) 已知函数
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若不等式 对任意
对任意 恒成立,求a的范围.
恒成立,求a的范围.