设函数 .
.
(1)当 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数;
(2)设函数 是奇函数,求
是奇函数,求 与
与 的值;
的值;
(3)在(2)条件下,判断并证明函数 的单调性,并求不等式
的单调性,并求不等式 的解集.
的解集.
(本小题满分12分)已知函数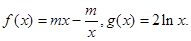
(1)当m=2时,求曲线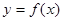 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;
(2)若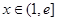 时,不等式
时,不等式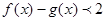 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分12分)请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.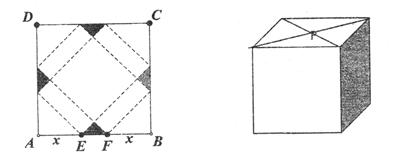
(本小题满分12分)已知 是递增的等差数列,满足
是递增的等差数列,满足
(1)求数列 的通项公式和前n项和公式;
的通项公式和前n项和公式;
(2)设数列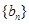 对
对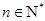 均有
均有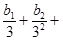 …+
…+ 成立,求数列
成立,求数列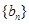 的通项公式.
的通项公式.
(本小题满分12分)如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,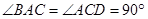 ,AE∥C
,AE∥C D,DC=AC=2AE=2.
D,DC=AC=2AE=2.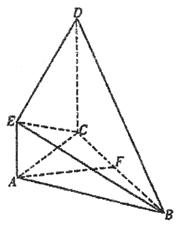
(Ⅰ)求证:平面BCD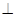 平面ABC
平面ABC
(Ⅱ)求证:AF∥平面BDE;
(Ⅲ)求四面体B-CDE的体积.
(本小题满分12分)
已知函数 且函数f(x)的最小正周期为
且函数f(x)的最小正周期为 .
.
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.若f(B)=1, 且
且 ,试求
,试求 的值.
的值.