统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: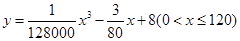 .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米.
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
已知函数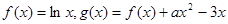 ,函数
,函数 的图像在点
的图像在点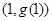 处的切线平行于
处的切线平行于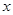 轴
轴
(1)求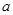 的值;
的值;
(2)求函数 的极值;
的极值;
(3)设斜率为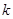 的直线与函数
的直线与函数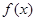 的图像交于两点
的图像交于两点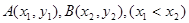 ,证明
,证明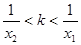 .
.
已知 其中
其中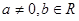
(1)求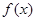 的单调区间;
的单调区间;
(2)设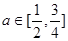 ,函数
,函数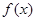 在区间
在区间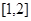 上的最大值为
上的最大值为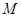 ,最小值为
,最小值为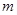 ,求
,求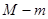 的取值范围.
的取值范围.
已知向量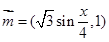 ,
,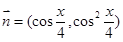 ,
,
(1)若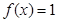 ,求
,求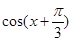 的值;
的值;
(2)在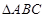 中,角
中,角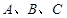 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数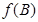 的取值范围.
的取值范围.
等差数列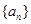 中,
中,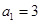 ,前
,前 项和为
项和为 ,等比数列
,等比数列 各项均为正数,
各项均为正数,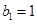 ,且
,且 ,
, 的公比
的公比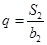
(1)求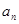 与
与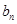 ;
; 
(2)求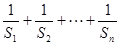 .
.
某同学用五点法画函数 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
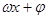 |
0 |
 |
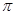 |
 |
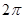 |
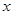 |
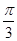 |
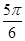 |
|||
 |
0 |
5 |
-5 |
0 |
(1)请将上表数据补充完整,并直接写出函数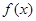 的解析式;
的解析式;
(2)若函数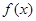 的图像向左平移
的图像向左平移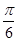 个单位后对应的函数为
个单位后对应的函数为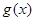 ,求
,求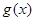 的图像离原点最近的对称中心.
的图像离原点最近的对称中心.