一企业生产的某产品在不做电视广告的前提下,每天销售量为b吨.经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量S(吨)与电视广告每天的播放量n(次)的关系可用如图所示的程序框图来体现.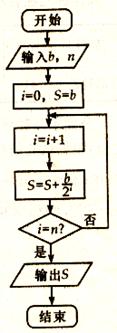
(1)试写出该产品每天的销售量S(吨)关于电视广告每天的播放量n(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加90%,则每天电视广告的播放量至少需多少次?
.(14分)已知椭圆 +
+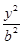 =1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足 =2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足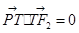 ,
,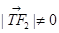
(1)设x为点P的横坐标,证明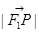 =a+
=a+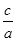 x;
x;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2?若存在,求∠F1MF2的正切值;若不存在,请说明理由.
设二次函数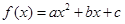 (a>0),方程
(a>0),方程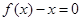 的两个根
的两个根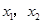
满足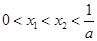 . (1)
. (1) ,求
,求 的值。
的值。
(2)设函数 的图象关于直线
的图象关于直线 对称,证明:
对称,证明:
(3)当x∈(0,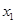 )时,证明x<
)时,证明x< <
<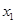 ;
;
、已知命题p:方程a2x2+ax-2=0在[-1,1]上有解:命题q:只有一个
实数 x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.
x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求a的取值范围.
.已知数列 满足
满足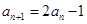 ,
, .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式和前
的通项公式和前 项和
项和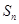 .
.
设函数
(1)求函数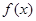 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当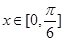 时,
时,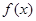 的最大值为2,求
的最大值为2,求 的值,并求出
的值,并求出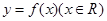 的对称
的对称
轴方程.