(1设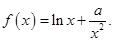
(1)当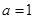
时，求f(x)的单调区间；
(2)求f(x)的零点个数
已知向量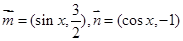
，设
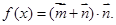
（1）求函数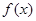
的表达式，并求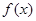的单调递减区间；
（2）在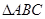
中，a，b，c分别是角A，B，C的对边，若
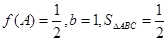，求a的值。
已知函数
（I）求
的极小值；
（II）若
上为单调增函数，求m的取值范围；
（III）设
（e是自然对数的底数）上至少存在一个
成立，求m的取值范围。
设椭圆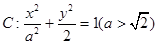
的左右焦点分别为F1，F2，A是椭圆C上第一象限内一点，
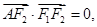坐标原点O到直线AF1的距离为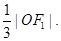
（I）求椭圆C的方程；
（II）设Q是椭圆C上的一点，过点Q的直线l交x轴于点
若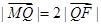
，求直线l的斜率。
若数列
，其中T为正整数，则称数列
为周期数列，其中T为数列的周期。
（I）设
是周期为7的数列，其中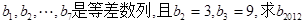
；
（II）设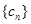
是周期为7的数列，其中
，对（I）中的数列
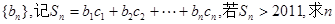的最小值。
正△ABC的边长为4，CD是AB边上的高，E，F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A—DC—B。
（I）试判断直线AB与平面DEF的位置关系，并说明理由；
（II）求二面角E—DF—C的余弦值；
（III）在线段BC上是否存在一点P，使AP⊥DE？证明你的结论。