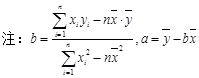(如图1)在平面四边形 中,
中, 为
为 中点,
中点, ,
, ,且
,且 ,现沿
,现沿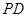 折起使
折起使 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.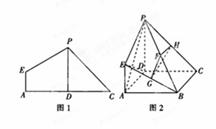
(1)求三棱锥 的体积;
的体积;
(2)在线段PC上是否存在一点M,使直线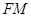 与直线
与直线 所成角为
所成角为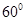 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.
(本题14分)口袋内有 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从
个白球.已知从
口袋中随机取出一个球是红球的概率是 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。
(Ⅰ)求 和
和 ;
;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 的分布列和期望
的分布列和期望 。
。
(本题14分)已知向量m = ,向量n =
,向量n = ,且m与n所成角为
,且m与n所成角为 ,其中A、B、C是
,其中A、B、C是 的内角。
的内角。
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围。
的取值范围。
若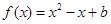 ,且
,且 ,
,
(1)求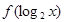 的最小值及相应 x的值;
的最小值及相应 x的值;
(2)若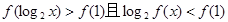 ,求x的取值范围.
,求x的取值范围.
已知函数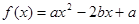 (
(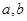
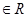 )
)
(1)若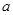 从集合
从集合 中任取一个元素,
中任取一个元素, 从集合
从集合 中任取一个元素,求方程
中任取一个元素,求方程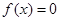 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 从区间
从区间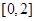 中任取一个数,
中任取一个数,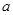 从区间
从区间 中任取一个数,求方程
中任取一个数,求方程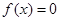 没有实根的概率.
没有实根的概率.
某车间为了规定工时定额,需要确定加共某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?