已知定义在 上的函数
上的函数 ,其中
,其中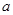 为常数.
为常数.
(1)当 是函数
是函数 的一个极值点,求
的一个极值点,求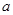 的值;
的值;
(2)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数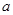 的取值范围;
的取值范围;
(3)当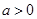 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数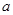 的取值范围.
的取值范围.
(本题14分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3m,AD=2m。
(1)设 (单位:m),要使花坛AMPN的面积大于32m2,求
(单位:m),要使花坛AMPN的面积大于32m2,求 的取值范围;
的取值范围;
(2)若 (单位:m),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:m),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
二次函数 满足
满足
(1)求 的解析式;
的解析式;
(2)在区间[-1,1]上,y= 的图象恒在
的图象恒在 的图象上方,试确定实数m的范围。
的图象上方,试确定实数m的范围。
已知函数
(1)求函数 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值;
(2)若 ,求
,求 的值。
的值。
命题p:函数 的定义域为R,命题q:不等式
的定义域为R,命题q:不等式 的解集为
的解集为 ,若“p∧q”为假命题且“p∨q”为真命题,求实数a的取值范围.
,若“p∧q”为假命题且“p∨q”为真命题,求实数a的取值范围.
(本题13分)
已知集合A={x| },B={x|x2>5-4x},C={x│|x-m|<1,m∈R}。
},B={x|x2>5-4x},C={x│|x-m|<1,m∈R}。
(1)求A∩B;
(2)若(A∩B) C,求m的取值范围。
C,求m的取值范围。