成都市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。若现有500人参加测试，学生成绩的频率分布直方图如下：
（I）求获得参赛资格的人数；
（II）根据频率直方图，估算这500名学生测试的平均成绩；
（III）若知识竞赛分初赛和复赛，在初赛中每人最多有3次选题答题的机会，累计答对2题或答错2题即终止，答对2题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
，求甲通过初赛的概率.
给定椭圆
，称圆心在坐标原点O，半径为
的圆是椭圆C的“伴随圆”，已知椭圆C的两个焦点分别是
.
（1）若椭圆C上一动点
满足
，求椭圆C及其“伴随圆”的方程；
（2）在（1）的条件下，过点
作直线l与椭圆C只有一个交点，且截椭圆C的“伴随圆”所得弦长为
，求P点的坐标；
（3）已知
，是否存在a，b，使椭圆C的“伴随圆”上的点到过两点
的直线的最短距离
.若存在，求出a，b的值；若不存在，请说明理由.
某种海洋生物身体的长度
（单位：米）与生长年限t（单位：年）
满足如下的函数关系：
.（设该生物出生时t=0）
（1）需经过多少时间，该生物的身长超过8米；
（2）设出生后第
年，该生物长得最快，求
的值.
已知函数
.
（1）若
，求实数x的取值范围；
（2）求
的最大值.
在△ABC中，BC=a，AC=b，a、b是方程
的两个根，且
，求△ABC的面积及AB的长.
已知函数
过点
.
（1）求实数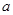
；
（2）将函数
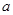的图像向下平移1个单位，再向右平移个单位后得到函数
图像，设函数关于
轴对称的函数为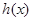
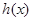，试求的解析式；
（3）对于定义在
上的函数
，若在其定义域内，不等式
恒成立，求实数
的取值范围.