.
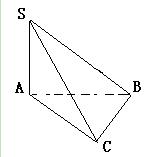
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=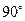 ,且AC=BC=5,SB=
,且AC=BC=5,SB= ,如图
,如图
(1)求侧面sBC与底面ABC所成二面角的大小
(2)求三棱锥的体积
成等差数列的三个正数的和等于9,且这三个数分别加上2,3,5后成为等比数列 中的
中的 (12分)
(12分)
(1)求数列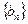 的通项公式
的通项公式
(2)求数列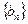 的前n项和
的前n项和
已知圆C: 内有一点P
内有一点P ,过点P作直线
,过点P作直线 交圆C与A,B两点
交圆C与A,B两点
(1)当 经过圆心C时,求直线
经过圆心C时,求直线 方程
方程
(2)当弦AB被点P平分时,求直线 方程
方程
(3)求过点(4,3)且与圆相切的直线方程
(本小题满分10分)设函数 (其中
(其中 >
>
0, ),且
),且 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求 的最小正周期;
的最小正周期;
(2)如果 在区间
在区间 上的最小值为
上的最小值为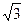 ,求a的值.
,求a的值.
(本小题满分10分)已知
 =
= ,
, =
= ,
,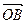 =
= ,设
,设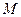 是直
是直
线 上一点,
上一点, 是坐标原点
是坐标原点
⑴求使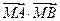 取最小值时的
取最小值时的 ;
; 
⑵对(1)中的点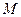 ,求
,求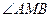 的余弦值。
的余弦值。