2014年11月10日APEC会议在北京召开，某服务部需从大学生中招收志愿者，被招收的志愿者需参加分笔试和面试两部分，把参加笔试的 40 名大学生的成绩分组： 第 1 组[75,80），第 2 组 [80,85），第 3 组[85, 90），第 4 组 [90, 95），第 5 组[95,100），得到频率分布直方图如图所示：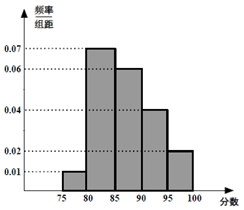
（Ⅰ）分别求成绩在第4，5组的人数；
（Ⅱ）现决定在笔试成绩较高的第 3，4，5 组中用分层抽样抽取 6 名进入面试，
①已知甲的成绩均在第4组，求甲进入面试的概率；
②若从这6名学生中随机抽取2名学生接受考官D的面试，设第3组中有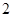
名学生被考官D面试的概率．
4个男生，3个女生站成一排。
（1）3个女生两两相邻，有多少种不同的站法。
（2）3个女生两两不相邻，有多少种不同的站法。
（3）男生甲不站排头，女生乙不站排尾有多少种不同
的站法。
（本小题满分10分）
在△ABC中，确A、B、C的对边分别为a、b、c，且a=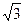
,b2+c2-
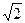bc=3。
（Ⅰ）求角A；
（Ⅱ）设cosB=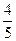
，求边c的大小。
（本小题满分12）
已知直线kx-y+1=0与双曲线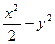
=1相交于两个不同的点A、B。
（Ⅰ）求k的取值范围；
（Ⅱ）若
x轴上的点M（3，0）到A、B两点的距离相等，求k的值。
（本小题满分12分）
已知函数f(x)=ax3+bx2+cx+d在（-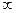
，1）上单调递减，在（1，3）上单调递增，在（3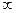，+）上单调递减、且函数图象在（2，f（2））处的切线与直线5x+y=0垂直。
（Ⅰ）求实数a、b、c的值；
（Ⅱ）设方程f(x)=0有三个不相等的实数根，求d的取值范围
。
（本小题满分12分）
数列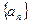
的前n项和记为Sn，已知a1=1,Sn=
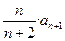,（n=1，2，3，……）
（Ⅰ）求数列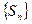
的通项公式；
（Ⅱ）设Tn=S1+S2+S3+……+Sn，求Tn