(本小题满分10分)
在△ABC中,确A、B、C的对边分别为a、b、c,且a=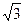 ,b2+c2-
,b2+c2-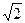 bc=3。
bc=3。
(Ⅰ)求角A;
(Ⅱ)设cosB=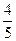 ,求边c的大小。
,求边c的大小。
已知等差数列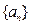 的公差
的公差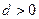 ,其前n项和为
,其前n项和为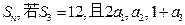 成等比数列.
成等比数列.
(I)求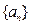 的通项公式;
的通项公式;
(II)记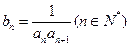 ,求数列
,求数列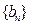 的前n项和
的前n项和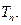
在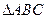 中,
中,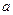 、
、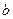 、
、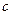 分别是角
分别是角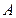 、
、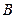 、
、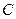 的对边,
的对边,
且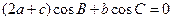 .
.
(Ⅰ)求角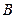 的值;
的值;
(Ⅱ)已知函数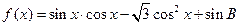 ,求
,求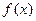 的单调递增区间
的单调递增区间
给出一个不等式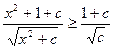 (x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
(x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
设 表示的区域为A,
表示的区域为A,
(1)在区域A中任取一点(x,y),求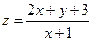 的取值范围;
的取值范围;
(2)平面上有一定点O(3,3),若一动点M满足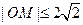 ,求点M落入区域A内的概率。
,求点M落入区域A内的概率。
某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层、每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x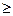 12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元),为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?
12)层,则每平方米的平均建筑费用为Q(x)=3000+50x(单位:元),为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?每平方米的平均综合费最小值是多少?