设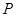 是圆
是圆 上的点,过
上的点,过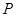 作直线
作直线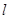 垂直
垂直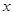 轴于点
轴于点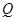 ,
,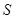 为
为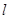 上一点,且
上一点,且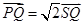 ,当点
,当点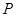 在圆上运动时,记点
在圆上运动时,记点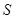 的轨迹为曲线
的轨迹为曲线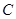 .
.
(Ⅰ)求曲线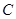 的方程;
的方程;
(Ⅱ)设动点 满足
满足 ,其中
,其中 是曲线
是曲线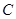 上的点,
上的点, 为原点,直线
为原点,直线 与
与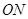 的斜率之积为
的斜率之积为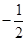 ,求证:
,求证: 为定值.
为定值.
如图,在平面直角坐标系 中,已知四边形
中,已知四边形 是等腰梯形,
是等腰梯形, ,点
,点 满足
满足 ,点
,点 在线段
在线段 上运动(包括端点).
上运动(包括端点).
(1)求 的余弦值;
的余弦值;
(2)是否存在实数 ,使
,使 ,若存在,求出满足条件的实数
,若存在,求出满足条件的实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分14分)某实验室某一天的温度(单位: )随时间t(单位:h)的变化近似满足函数关系:
)随时间t(单位:h)的变化近似满足函数关系: ,
, .
.
(1)求实验室这一天里,温度降低的时间段;
(2)若要求实验室温度不高于10 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
已知函数 .
.
(1)求函数 单调区间;
单调区间;
(2)若在区间 上,
上, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
(本小题满分14分)已知函数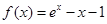 ,
, , 其中,
, 其中,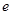 是自然对数的底数.函数
是自然对数的底数.函数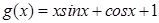 ,
,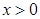 .
.
(Ⅰ)求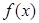 的最小值;
的最小值;
(Ⅱ)将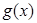 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列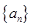 ,求证:
,求证:
(1)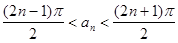 ,其中
,其中 ;
;
(2)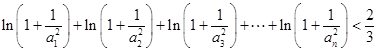 .
.