已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求 的最小值.
的最小值.
(本小题满分12分)
设函数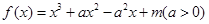 .
.
(1)若函数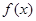 在
在 内没有极值点,求实数
内没有极值点,求实数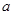 的取值范围;
的取值范围;
(2) 时函数
时函数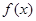 有三个互不相同的零点,求实数
有三个互不相同的零点,求实数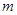 的取值范围;
的取值范围;
(3)若对任意的 ,不等式
,不等式 在
在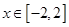 上恒成立,求实数
上恒成立,求实数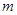 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.
(1)求椭圆的方程;
(2)设过定点M(0,2)的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率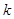 的取值范围.
的取值范围.
(本小题满分12分)
甲乙两位学生参加数学竞赛培训,在培训期间他们参加5次预赛成绩记录如下:
甲: 78 76 74 90 82
乙: 90 70 75 85 80
(1)用茎叶图表示这两组数据;
(2)从甲乙两人成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
(本小题满分12分)
在四棱锥 中,侧面
中,侧面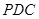 是边长为2的正三角形,且与底面垂直;底面
是边长为2的正三角形,且与底面垂直;底面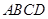 是菱形,
是菱形, ,
,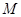 为
为 的中点.
的中点.
(1)求四棱锥 的体积;
的体积;
(2)求证: 平面
平面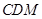 .
.
(本小题满分12分)
若平面向量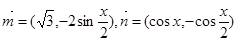 (
(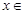 R),函数
R),函数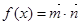 .
.
(1)求函数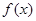 的值域;
的值域;
(2)记△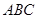 的内角
的内角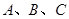 的对边长分别为
的对边长分别为 ,若
,若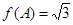 ,且
,且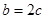 ,求角
,求角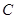 的值.
的值.