在方向水平的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点。把小球拉起直至细线与场强平行,然后无初速释放。已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ(如图)。求小球经过最低点时细线对小球的拉力。
在一列火车上放一杯水,火车静止和匀速运动时,水的内能是否变化?
有人设计了一种测温装置,其结构如图所示.玻璃泡A内封有一定量气体,与管A相连的B管插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出.设B管的体积与A泡的体积相比可略去不计.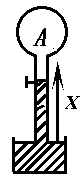
(1)标准大气压下对B管进行温度刻度(标准大气压相当于76cm水银柱的压强).已知当温度t=27℃的刻度线,x=16cm.问t=0℃的刻度线在x为多少厘米处?
(2)若大气压已变为相当于75cm水银柱的压强,利用该测温装置测量温度时所得读数仍为27℃,问此时实际温度为多少?
图中竖直圆筒是固定不动的,粗筒横截面积是细筒的4倍,细筒足够长,粗筒中A、B两轻质活塞间封有空气,气柱长1=20cm.活塞A上方的水银深H=10cm,两活塞与筒壁间的摩擦不计.用外力向上托住活塞B,使之处于平衡状态,水银面与粗筒上端相平,现使活塞缓慢上移直至水银的一半被推入细筒中,求活塞B上移的距离.设在整个过程中气柱的温度不变,大气压强P0相当于75cm高的水银柱产生的压强.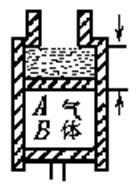
一个密闭的气缸,被活塞分成体积相等的左右两室,气缸壁与活塞是不导热的,它们之间没有摩擦,两室中气体的温度相等,如图所示,现利用右室中的电热丝对右室中的气体加热一段时间,达到平衡后,左室的体积变为原来体积的 ,左室气体的温度T1=300K,求右室气体的温度.
,左室气体的温度T1=300K,求右室气体的温度.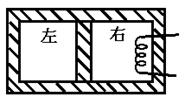
图中A、B是体积相同的气缸,B内有一导热的,可在气缸内无摩擦滑动的、体积不计的活塞C,D为不导热的阀门,起初,阀门关闭,A内装有压强P1=2.0×105Pa,温度T1=300K的氮气,B内装有压强P2=1.0×105Pa,温度T2=600K的氧气.阀门打开后,活塞C向右移动,最后达到平衡以V1和V2表示平衡后的氮气和氧气的体积,则V1∶V2的值是多少?.(假设氧气和氮气均为理想气体,并与外界无热交换,连接气缸的管道体积可忽略.)