如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点．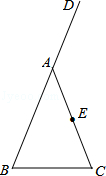
（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）．
①作∠DAC的平分线AM． ②连接BE并延长交AM于点F．
（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．
先化简，后求值：
，其中
=－4．
如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于O，AC=BD．
求证：（1）BC=AD；
（2）△OAB是等腰三角形．
从1名男生和2名女生中随机抽取参加“我爱我家乡”演讲赛的学生，求下列事件的概率：
（1）抽取1名，恰好是男生；
（2）抽取2名，恰好是1名女生和1名男生．
如图，在平面直角坐标系中，直线
：y=－2x＋b (b≥0)的位置随b的不同取值而变化．
(1)已知⊙M的圆心坐标为(4，2)，半径为2．
当b= 时，直线：y=－2x＋b (b≥0)经过圆心M：
当b= 时，直线：y=－2x＋b(b≥0)与OM相切：
(2)若把⊙M换成矩形ABCD，其三个顶点坐标分别为：A(2，0)、B（6，0）、C(6，2).
设直线扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式，
如图，已知△ABC的三个顶点坐标分别为A(－4，0)、B(1，0)、C(－2，6)．
(1)求经过A、B、C三点的抛物线解析式；
(2)设直线BC交y轴于点E，连接AE，求证：AE=CE;
(3)设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F，为顶点的三角形与△ABC相似吗？
请说明理由．