已知椭圆C: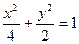 上动点
上动点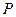 到定点
到定点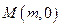 ,其中
,其中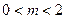 的距离
的距离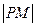 的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线
的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线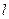 ,使
,使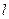 与椭圆C的两个交点A、B满足条件
与椭圆C的两个交点A、B满足条件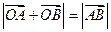 (O为原点),若存在,求出
(O为原点),若存在,求出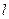 的方程,若不存在请说是理由。
的方程,若不存在请说是理由。
(1)(2005全国卷1)已知椭圆的中心为坐标原点O,焦点在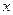 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,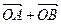 与
与 共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且
共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且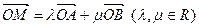 ,证明
,证明 为定值。
为定值。
设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则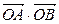 等于()
等于()
A.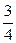 |
B.-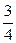 |
C.3 | D.-3 |
(03年新课程高考)已知常数a>0,向量c=(0,a),i=(1,0),经过原点O以c+λi为方向向量的直线与经过定点A(0,a)以i-2λc为方向向量的直线相交于点P,其中λ∈R.试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
若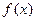 在定义域(-1,1)内可导,且
在定义域(-1,1)内可导,且 ,点A(1,
,点A(1,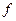 (
(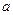 ));B(
));B(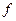 (-
(-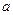 ),1),
),1),
对任意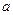 ∈(-1,1)恒有
∈(-1,1)恒有 成立,试在
成立,试在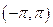 内求满足不等式
内求满足不等式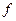 (sin
(sin cos
cos )+
)+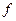 (cos2
(cos2 )>0的
)>0的 的取值范围.
的取值范围.