(本小题满分12分)
已知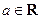 ,函数
,函数 .
.
(1)若函数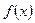 在区间
在区间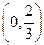 内是减函数,求实数
内是减函数,求实数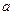 的取值范围;
的取值范围;
(2)求函数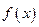 在区间
在区间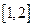 上的最小值
上的最小值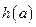 ;
;
(3)对(2)中的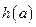 ,若关于
,若关于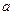 的方程
的方程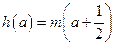 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数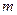 的取值范围.
的取值范围.
设函数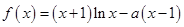 在
在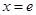 处的切线与
处的切线与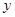 轴相交于点
轴相交于点 .
.
(1)求 的值;
的值;
(2)函数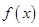 能否在
能否在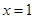 处取得极值?若能取得,求此极值;若不能,请说明理由;
处取得极值?若能取得,求此极值;若不能,请说明理由;
(3)当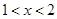 时,试比较
时,试比较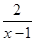 与
与 大小.
大小.
设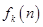 为关于
为关于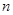 的
的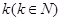 次多项式,数列
次多项式,数列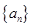 的首项
的首项 ,前
,前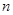 项和为
项和为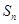 ,对于任意的正整数
,对于任意的正整数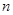 ,
,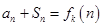 都成立.
都成立.
(1)若 ,求证:数列
,求证:数列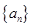 是等比数列;
是等比数列;
(2)试确定所有的自然数 ,使得数列
,使得数列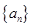 能成等差数列.
能成等差数列.
如图,在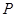 地正西方向
地正西方向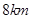 的
的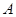 处和正东方向
处和正东方向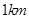 的
的 处各有一条正北方向的公路
处各有一条正北方向的公路 和
和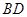 ,现计划在
,现计划在 和
和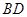 路边各维修一个物流中心
路边各维修一个物流中心 和
和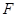 ,为缓解交通压力,决定修建两条互相垂直的公路
,为缓解交通压力,决定修建两条互相垂直的公路 和
和 ,设
,设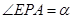
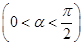 .
.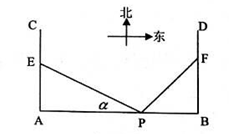
(1)为减少对周边区域的影响,试确定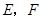 的位置,使
的位置,使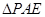 和
和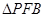 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定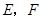 的位置,使
的位置,使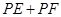 的值最小.
的值最小.
如图,在四棱锥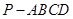 中,
中, 底面
底面 ,
, 为直角,
为直角, ,
, ,
, 分别为
分别为 的中点.
的中点.
(1)试证: 平面
平面 ;
;
(2)设 ,且二面角
,且二面角 的平面角大于
的平面角大于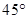 ,求
,求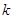 的取值范围.
的取值范围.
在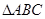 中,角
中,角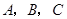 所对的边分别为
所对的边分别为 ,满足
,满足 ,且
,且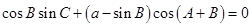 .
.
(1)求角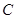 的大小;
的大小;
(2)求 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的值.
的值.