已知抛物线 的顶点为原点,其焦点
的顶点为原点,其焦点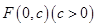 到直线
到直线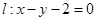 的距离为
的距离为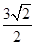 .设
.设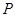 为直线
为直线 上的点,过点
上的点,过点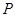 作抛物线
作抛物线 的两条切线
的两条切线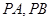 ,其中
,其中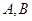 为切点.
为切点.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)设点 为直线
为直线 上的点,求直线
上的点,求直线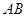 的方程;
的方程;
(Ⅲ) 当点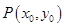 在直线
在直线 上移动时,求
上移动时,求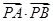 的最小值.
的最小值.
人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第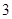 次拨号才接通电话;
次拨号才接通电话;
(2)拨号不超过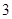 次而接通电话.
次而接通电话.
设袋中有N个球,其中有M个红球,N-M个黑球,从中任取n个球,问恰有k个红球的概率是多少?
一批产品共100件,其中有10件次品,为了检验其质量,从中随机抽取5件,求在抽取的这5件产品中次品数的分布列,并说明5件产品中有3件以上为次品的概率.(精确到0.001)
由180只集成电路组成的一批产品中,有8只是次品,现从中任抽4只,用 表示其中的次品数,试求:
表示其中的次品数,试求:
(1)抽取的4只中恰好有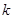 只次品的概率;
只次品的概率;
(2)抽取的4只产品中次品超过1只的概率.
交5元钱,可以参加一次摸奖,一袋中有同样大小的球10个,其中8个标有1元钱,2个标有5元钱,摸奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和,求抽奖人所得钱数的分布列.