已知曲线 的参数方程是
的参数方程是 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为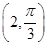 .
.
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求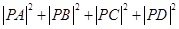 的取值范围.
的取值范围.
已知函数 .
.
(1)求不等式 的解集;
的解集;
(2)设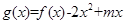 ,其中
,其中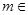 R,求
R,求 在区间
在区间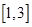 上的最小值.
上的最小值.
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100m,∠BAC=60°,在A地听到弹射声音的时间比B地晚 s.A地测得该仪器在C处时的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(声音的传播速度为340m/s)
s.A地测得该仪器在C处时的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(声音的传播速度为340m/s)
设函数 .
.
(1)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(2)设A、B、C为△ABC的三个内角,若 且C为锐角,求sinA的值.
且C为锐角,求sinA的值.
设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 ,对
,对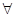
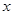 ∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数
∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数 的取值范围.
的取值范围.
已知二次函数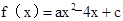 .若
.若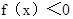 的解集是
的解集是
(1)求实数 的值;
的值;
(2)求函数 在
在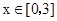 上的值域.
上的值域.