已知函数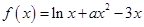 ,且在
,且在 时函数取得极值.
时函数取得极值.
(1)求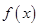 的单调增区间;
的单调增区间;
(2)若 ,
,
(Ⅰ)证明:当 时,
时,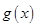 的图象恒在
的图象恒在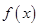 的上方;
的上方;
(Ⅱ)证明不等式 恒成立.
恒成立.
已知函数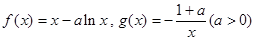 .
.
(Ⅰ)若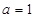 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)设函数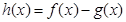 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
如图,在五面体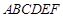 中,四边形
中,四边形 是边长为4的正方形,
是边长为4的正方形, ,平面
,平面
 平面
平面 ,且
,且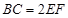 ,
,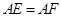 ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明: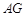
 平面
平面 ;
;
(Ⅱ)若直线BF与平面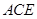 所成角的正弦值为
所成角的正弦值为 ,求
,求 的长;
的长;
(Ⅲ)判断线段 上是否存在一点
上是否存在一点 ,使
,使 //平面
//平面 ?若存在,求出
?若存在,求出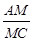 的值;若不存在,说明理由.
的值;若不存在,说明理由.
某大学志愿者协会有10名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为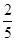 .
.
| 专业 性别 |
中文 |
英语 |
数学 |
体育 |
| 男 |
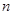 |
1 |
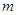 |
1 |
| 女 |
1 |
1 |
1 |
1 |
现从这10名同学中随机选取3名同学参加社会公益活动(每位同学被选到的可能性相同).
(Ⅰ)求 的值;
的值;
(Ⅱ)求选出的3名同学恰为专业互不相同的男生的概率;
(Ⅲ)设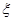 为选出的3名同学中“女生或数学专业”的学生的人数,求随机变量
为选出的3名同学中“女生或数学专业”的学生的人数,求随机变量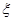 的分布列及其数学期望
的分布列及其数学期望 .
.
设函数 ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 的值域;
的值域;
(Ⅱ)已知函数 的图象与直线
的图象与直线 有交点,求相邻两个交点间的最短距离.
有交点,求相邻两个交点间的最短距离.
已知函数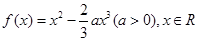 .
.
(1)求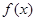 的单调区间和极值;
的单调区间和极值;
(2)若对于任意的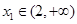 ,都存在
,都存在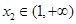 ,使得
,使得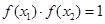 ,求
,求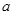 的取值范围.
的取值范围.