某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为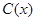 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,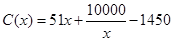 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润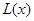 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
如图所示,在四棱锥 中,
中,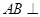 平面
平面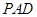 ,
,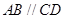 ,
, ,
,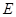 是
是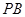 的中点,
的中点, 是
是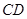 上的点且
上的点且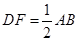 ,
,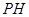 为△
为△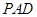 中
中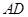 边上的高.
边上的高.
(1)证明: 平面
平面 ;
;
(2)若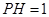 ,
, ,
,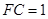 ,求三棱锥
,求三棱锥 的体积;
的体积;
(3)证明: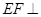 平面
平面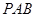 .
.
下图是淮北市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择6月1日至6月15日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气重度污染的概率;
(2)若设 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
(3)由图判断从哪天开始淮北市连续三天的空气质量指数方差最大?(结论不要求证明)
如图,在△ABC中,∠ABC=90°,AB=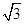 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB=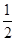 ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
已知函数f(x)=4cos ωx· (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间 上的单调性.
上的单调性.
设全集 .
.
(1)解关于x的不等式 ;
;
(2)记A为(1)中不等式的解集,集合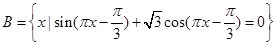 ,若
,若 恰有3个元素,求
恰有3个元素,求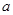 的取值范围.
的取值范围.