在直角坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线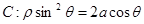
 ,已知过点
,已知过点 的直线
的直线 的参数方程为
的参数方程为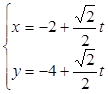 (
( 为参数),直线
为参数),直线 与曲线
与曲线 分别交于
分别交于 两点.
两点.
(Ⅰ)写出曲线 和直线
和直线 的普通方程;
的普通方程;
(Ⅱ)若 成等比数列,求
成等比数列,求 的值.
的值.
设
均为正数,且
,证明:
(Ⅰ)
;
(Ⅱ)
已知动点 , 都在曲线C: ( 为参数)上,对应参数分别为 与 ( ), 为 的中点。
(Ⅰ)求
的轨迹的参数方程
(Ⅱ)将
到坐标原点的距离
表示为
的函数,并判断
的轨迹是否过坐标原点。
如图,
为
外接圆的切线,
的延长线交直线
于点
,
分别为弦
与弦
上的点,且
四点共圆.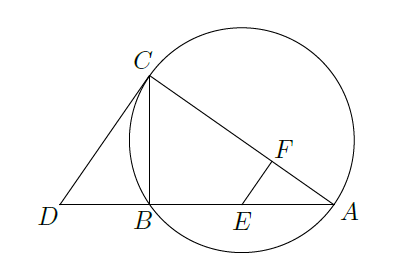
证明:
(Ⅰ)
是
外接圆的直径;
(Ⅱ)若
.求过
四点的圆的面积与
外接圆面积的比值.
己知函数
.
(I)求
的极小值和极大值;
(II)当曲线
的切线
的斜率为负数时,求
在
轴上截距的取值范围.
在平面直角坐标系
中,己知圆
在
上截得线段长为
,在
轴上截得线段长为
.
(Ⅰ)求圆心
的轨迹方程;
(Ⅱ)若
点到直线
的距离为 ,求圆
的方程.
,求圆
的方程.