如图,在直角坐标系xOy中,锐角△ABC内接于圆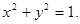 已知BC平行于x轴,AB所在直线方程为
已知BC平行于x轴,AB所在直线方程为 ,记角A,B,C所对的边分别是a,b,c.
,记角A,B,C所对的边分别是a,b,c.
(1)若 的值;
的值;
(2)若 的值.
的值.
已知二次函数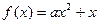 (
(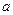
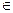 R,
R,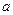
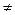 0).
0).
(Ⅰ)当0<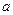 <
<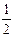 时,
时,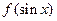 (
(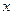
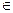 R)的最大值为
R)的最大值为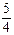 ,求
,求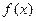 的最小值.
的最小值.
(Ⅱ)如果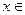 [0,1]时,总有|
[0,1]时,总有|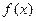 |
|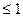 .试求
.试求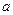 的取值范围.
的取值范围.
(Ⅲ)令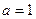 ,当
,当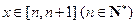 时,
时,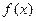 的所有整数值的个数为
的所有整数值的个数为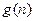 ,求数列
,求数列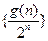 的前
的前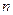 项的和
项的和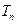 .
.
记函数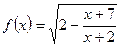 的定义域
的定义域
为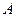 ,
,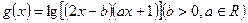 的定义域为
的定义域为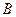 ,
,
(1)求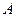 :
:
(2)若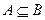 ,求
,求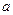 、
、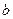 的取值范围
的取值范围
设函数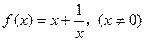 的图象为
的图象为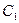 、
、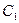 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为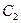
 ,
,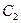 对应的函数为
对应的函数为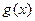 .
.
(1)求函数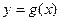 的解析式;
的解析式;
(2)若直线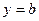 与
与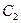 只有一个交点,求
只有一个交点,求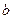 的值并求出交点的坐标.
的值并求出交点的坐标.
对于函数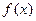 ,若存在
,若存在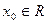 ,使
,使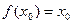 成立,则称点
成立,则称点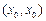 为函数的不动点。
为函数的不动点。
(1)已知函数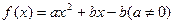 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求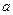 与
与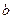 的值;
的值;
(2)若对于任意实数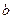 ,函数
,函数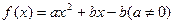 总有两个相异的不动点,求
总有两个相异的不动点,求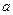 的取值范围;
的取值范围;
(3)若定义在实数集R上的奇函数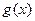 存在(有限的)
存在(有限的)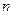 个不动点,求证:
个不动点,求证: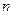 必为奇数。
必为奇数。
函数
⑴求证: 的图像关于直线y=x对称;
的图像关于直线y=x对称;
⑵函数 的图像与函数
的图像与函数 的图像有且只有一个交点,求实数
的图像有且只有一个交点,求实数 的值;
的值;
⑶是否存在圆心在原点的圆与函数 的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。
的图象有且只有三个交点,如果存在,则求出此圆的半径;如果不存在,请说明理由。