如图,圆 :
: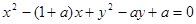 .
.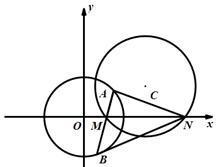
(Ⅰ)若圆 与
与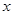 轴相切,求圆
轴相切,求圆 的方程;
的方程;
(Ⅱ)已知 ,圆C与
,圆C与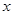 轴相交于两点
轴相交于两点 (点
(点 在点
在点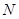 的左侧).过点
的左侧).过点 任作一条直线与圆
任作一条直线与圆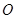 :
: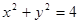 相交于两点
相交于两点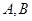 .问:是否存在实数
.问:是否存在实数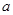 ,使得
,使得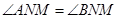 ?若存在,求出实数
?若存在,求出实数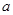 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
设已知函数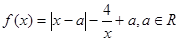 ,
,
(1)当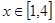 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式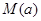
(2)是否存在实数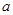 ,使得
,使得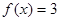 有且仅有3个不等实根,且它们成等差数列,若存在,求出所有
有且仅有3个不等实根,且它们成等差数列,若存在,求出所有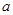 的值,若不存在,说明理由.
的值,若不存在,说明理由.
在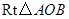 中,
中,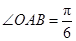 ,斜边
,斜边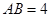 .
.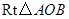 以直线
以直线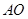 为轴旋转得到
为轴旋转得到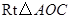 ,且二面角
,且二面角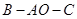 是直二面角,动点
是直二面角,动点 在斜边
在斜边 上.
上.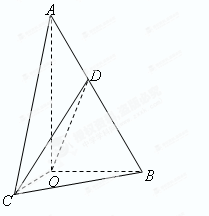
(1)求证:平面 平面
平面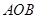 ;
;
(2)当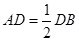 时,求异面直线
时,求异面直线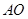 与
与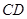 所成角的正切值;
所成角的正切值;
(3)求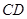 与平面
与平面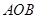 所成最大角的正切值.
所成最大角的正切值.
已知数列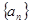 的前
的前 项和为
项和为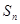 ,已知
,已知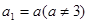 ,
,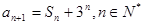 .
.
(1)设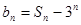 ,求证:数列
,求证:数列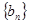 是等比数列,并写出数列
是等比数列,并写出数列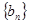 的通项公式;
的通项公式;
(2)若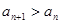 对任意
对任意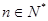 都成立,求实数
都成立,求实数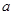 的取值范围.
的取值范围.
(本小题满分15分)
在 中,角
中,角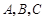 所对的边分别为
所对的边分别为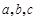 .已知
.已知 .
.
(1)若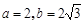 .求
.求 的面积;
的面积;
(2)求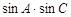 的取值范围.
的取值范围.
【选修4-5:不等式选讲】
设函数f(x)=|2x﹣1|﹣|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.