已知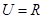 ,集合
,集合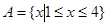 ,
,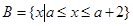 .
.
(Ⅰ)若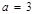 ,求
,求 ,
,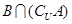 ;
;
(Ⅱ)若 ,求
,求 的范围.
的范围.
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝.再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).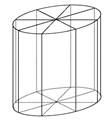
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).
已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.
(1)画出该三棱锥的直观图.
(2)求出侧视图的面积.
用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台的母线长.
一矩形铁皮的长为8 cm,宽为5 cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大?
设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若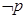 是
是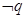 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.