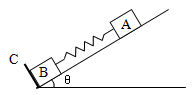
如图所示,在倾角为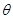 的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量分别为
的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们的质量分别为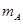 、
、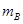 ,弹簧的劲度系数为
,弹簧的劲度系数为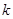 ,C为一固定挡板,系统处于静止状态.现开始用一恒力
,C为一固定挡板,系统处于静止状态.现开始用一恒力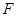 沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A的加速度
沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A的加速度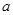 和从开始到此时物块A的位移
和从开始到此时物块A的位移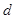 .(重力加速度为
.(重力加速度为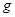 )
)
如图所示,质量m=4kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.4,传送带的长度l=6m,当传送带以v=4m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°。已知:g="10" m/s2,sin37°="0.6," cos37°=0.8。求: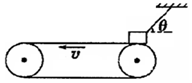
(1)传送带稳定运动时绳子的拉力T;
(2)某时刻剪断绳子,则经过多少时间,物体可以运动到传送带的左端。
(12分)如下图所示,初速度为零的负离子经电势差为U的匀强电场加速后,从离子枪T
中水平射出,经过一段路程后进入水平放置的距离为d的两平行金属板MN和PQ之间,
离子所经空间存在着磁感应强度为B的匀强磁场.不考虑离子重力作用,离子的荷质比 在什么范围内,离子才能打在金属板PQ上?
在什么范围内,离子才能打在金属板PQ上?
如下图所示,把总电阻为2R的均匀电阻丝焊接成一半径为a的圆环,水平固定在竖直向下的磁感应强度为B的匀强磁场中,一长度为2a,电阻等于R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的接触.当金属棒以恒定速度v向右移动经过环心O时,求:
(1)棒上电流的大小和方向及棒两端的电压UMN;
(2)在圆环和金属棒上消耗的总热功率.
如下图所示,匀强电场中A、B、C三点构成一个直角三角形,把电荷量q=-2×10-10C的点电荷由A点移动到B点,电场力做功4.8×10-8 J,再由B点移到C点电荷克服电场力做功4.8×10-8 J,取B点的电势为零,求A、C两点的电势及匀强电场的场强方向.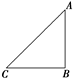
如下图所示,线圈abcd每边长l=0.20 m,线圈质量m1=0.10 kg,电阻R=0.10 Ω ,砝码质量m2=0.14 kg.线圈上方的匀强磁场的磁感应强度B=0.5 T,方向垂直线圈平面向里,磁场区域的宽度为h=l=0.20 m.砝码从某一位置下降,使ab边进入磁场开始做匀速运动.求线圈做匀速运动的速度大小. 