设函数 ,其中
,其中 .
.
(I)若函数 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线 的对称点在
的对称点在 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当 时,设
时,设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设 ,曲线
,曲线 上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
如图,某市准备在一个湖泊的一侧修建一条直路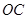 ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段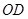 是以
是以 为顶点,
为顶点, 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段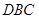 是函数
是函数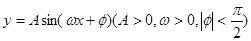 ,
,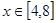 时的图象,图象的最高点为
时的图象,图象的最高点为 ,
, ,垂足为
,垂足为 .
.
(1)求函数 的解析式;
的解析式;
(2)若在湖泊内修建如图所示的矩形水上乐园 ,问:点
,问:点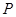 落在曲线
落在曲线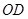 上何处时,水上乐园的面积最大?
上何处时,水上乐园的面积最大?
设函数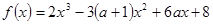 ,其中
,其中 .
.
(1)若 在
在 处取得极值,求常数
处取得极值,求常数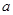 的值;
的值;
(2)设集合 ,
,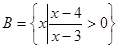 ,若
,若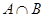 元素中有唯一的整数,求
元素中有唯一的整数,求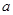 的取值范围.
的取值范围.
已知函数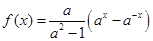 ,其中
,其中
(1)写出 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明);
(2)若函数 的定义域为
的定义域为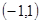 ,求满足不等式
,求满足不等式 的实数
的实数 的取值集合;
的取值集合;
(3)当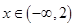 时,
时,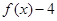 的值恒为负,求
的值恒为负,求 的取值范围.
的取值范围.
已知函数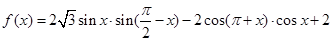 .
.
(1)求 的最小正周期;
的最小正周期;
(2)在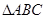 中,
中,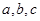 分别是
分别是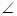 A、
A、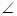 B、
B、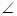 C的对边,若
C的对边,若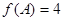 ,
, ,
,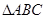 的面积为
的面积为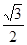 ,求
,求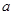 的值.
的值.
设函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .(1)求
.(1)求 ;(2)若
;(2)若 ,
, ,求实数
,求实数 的取值范围.
的取值范围.