如图,直三棱柱 中,
中, ,
, 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO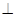 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:(1)PA∥平面BDE;
(2)平面EBD⊥平面PAC

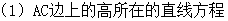 ;
;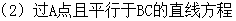 。
。
(3)求BC边的高
已知函数 (
( ,
, ).
).
(1)若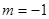 时,判断函数
时,判断函数 在
在 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)若对于定义域内一切 ,
, 恒成立,求实数
恒成立,求实数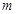 的值;
的值;
(3)在 (2)的条件下,当
(2)的条件下,当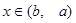 时,
时, 的取值恰为
的取值恰为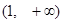 ,求实数
,求实数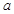 ,
,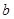 的值.
的值.
已知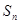 是数列
是数列 的前
的前 项和,
项和, (
( ,
,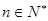 ),且
),且 .
.
(1)求 的值,并写出
的值,并写出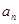 和
和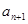 的关系式;
的关系式;
(2)求数列 的通项公式及
的通项公式及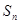 的表达式;
的表达式;
( 3)我们可以证明:若数列
3)我们可以证明:若数列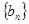 有上界(即存在常数
有上界(即存在常数 ,使得
,使得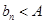 对一切
对一切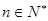 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列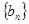 有下界(即存在常数
有下界(即存在常数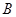 ,使得
,使得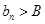 对一切
对一切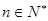 恒成立)且单调递减,则
恒成立)且单调递减,则 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: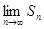 存在.
存在.
(1)求以 为渐近线,且过点
为渐近线,且过点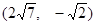 的双曲线
的双曲线 的方程;
的方程;
(2)求以双曲线 的顶点为焦点,焦点为顶点的椭圆
的顶点为焦点,焦点为顶点的椭圆 的方程;
的方程;
(3)椭圆 上有两点
上有两点 ,
, ,
,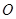 为坐标原点,若直线
为坐标原点,若直线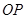 ,
,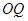 斜率之积为
斜率之积为 ,求证:
,求证: 为定值
为定值