如图,一条笔直的小路CA通向河边的一座凉亭A,小路与河边成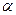 角(
角(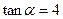 ),在凉亭北偏东45
),在凉亭北偏东45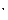 方向
方向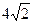 cm处的B处有一颗千年古树。现准备从小路的某点P处开挖新修一条直路P
cm处的B处有一颗千年古树。现准备从小路的某点P处开挖新修一条直路P D经过古树通向河边,两条路与河边围成的区域种上草坪。当开挖点P选在距凉亭多远处能使草坪占地面积最小?
D经过古树通向河边,两条路与河边围成的区域种上草坪。当开挖点P选在距凉亭多远处能使草坪占地面积最小?
在梯形ABCD中AB∥CD,AD=DC=CB=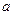 ,
, ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=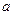 .
.
(1)求证:BC⊥平面ACFE;
(2)求EC与平面BEF所成角的正弦值.
已知直线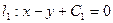 ,
,
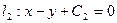 ,
, ,……,
,……, (其中
(其中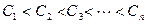 ),当
),当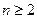 时,直线
时,直线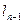 与
与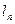 间的距离为n.
间的距离为n.
(1)求 ;
;
(2)求直线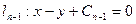 与直线
与直线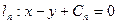 及x轴、y轴围成图形的面积.
及x轴、y轴围成图形的面积.
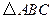 的周长为
的周长为 ,且
,且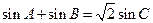 .
.
(1)求边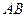 的长;
的长;
(2)若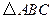 的面积为
的面积为 ,求角
,求角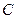 的度数.
的度数.
设椭圆 的左、右焦点分别为F1与
的左、右焦点分别为F1与
F2,直线 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。
(1)求椭圆C的方程;
(2)设椭圆C经过伸缩变换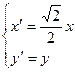 变成曲线
变成曲线 ,直线
,直线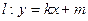 与曲线
与曲线 相切
相切
且与椭圆C交于不同的两点A、B,若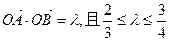 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)