某幼儿园在“六·一儿童节”开展了一次亲子活动，此次活动由宝宝和父母之一（后面以家长代称）共同完成，幼儿园提供了两种游戏方案：
方案一 宝宝和家长同时各抛掷一枚质地均匀的正方体骰子（六个面的点数分别是1，2，3，4，5，6），宝宝所得点数记为
,家长所得点数记为
;
方案二 宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间［1，6］的随机实数)，宝宝的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为
.
（Ⅰ）在方案一中，若
,则奖励宝宝一朵小红花，求抛掷一次后宝宝得到一朵小红花的概率；
（Ⅱ）在方案二中，若
,则奖励宝宝一本兴趣读物，求按下一次按钮后宝宝得到一本兴趣读物的概率.
甲乙两物体分别从相距70米的两处同时运动，甲第一分钟走2米，以后每分钟比前一分钟多走1米，乙每分钟走5米。
（1）.甲乙开始运动后几分钟相遇？
（2）如果.甲乙到达对方起点后立即折返，甲继续每分钟比前一分钟多走1米，乙继续每分钟走5米，那么开始运动几分钟后第二次相遇。
已知函数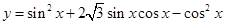
，
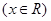
（1）求最小正周期（2）单调增区间
（3）
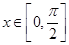时，求函数的值域。
设数列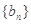
满足：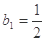
，
(Ⅰ)求证：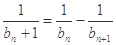
；
(Ⅱ)若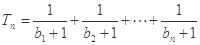
，对任意的正整数
，
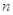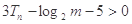恒成立,
求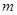
的取值范围.
在海岸A处，发现北偏东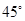
方向，距离A为
海里的B处有一走私船，在A北偏西
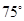方向距离A为2海里的C处有我方一艘缉私艇奉命以
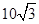海里/小时的速度追截走私船，且C在B的正西方，此时走私船正以
海里/小时的速度从B处向北偏东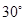
方向逃窜，问缉私艇沿什么方向，才能最快追上走私船？需要多长时间？
已知锐角三角形ABC中，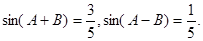
（Ⅰ）求证：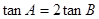
；
（Ⅱ）设AB=3，求AB边上的高