已知椭圆
的离心率为
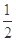，以原点为圆心，椭圆的短半轴为半径的圆与直线
相切，过点P（4，0）且不垂直于x轴直线
与椭圆C相交于A、B两点.
（1）求椭圆C的方程；
（2）求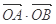
的取值范围；
（3）若B点关于x轴的对称点是E，证明：直线AE与x轴相交于定点.
已知函数
，
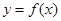在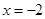
时有极值，在
处的切线方程为
．
（1）求a，b，c
（2）求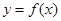在
上的最大值．
通过市场调查，得到某种产品的资金投入x万元与获得的利润y万元的数据，如表所示：
（1）根据上表提供的数据，用最小二乘法求线性回归方程；
（2）现投入资金10万元，求获得利润的估计值为多少万元？
（参考公式：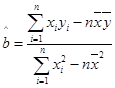
，
）
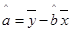设函数
（1）证明：
；
（2）若
，求m的取值范围．
在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ（sinθ+cosθ）=1，曲线C2的参数方程为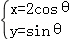
（θ为参数）．
（Ⅰ）求曲线C1的直角坐标方程与曲线C2的普通方程；
（Ⅱ）试判断曲线C1与C2是否存在两个交点？若存在，求出两交点间的距离；若不存在，说明理由．
如图，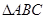
为直角三角形，
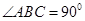，以AB为直径的圆交AC与点E，点D是BC边的中点，连接OD交圆于点M，求证：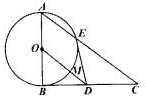
（1）O、B、D、E四点共圆；
（2）
．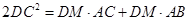