某工厂甲、乙两个车间包装同一种产品，在自动包装传送带上每隔
小时抽一包产品，称其重量（单位：克）是否合格，分别记录抽查数据，获得重量数据的茎叶图如图所示.
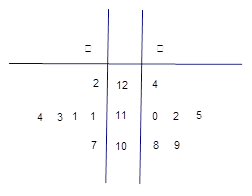
（1）根据样品数据，计算甲、乙两个车间产品重量的平均值与方差，并说明哪个车间的产品的重量相对较稳定；
（2）若从乙车间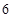
件样品中随机抽取两件，求所抽取的两件样品的重量之差不超过
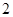克的概率.
某牛奶厂2002年初有资金1000万元，由于引进了先进生产设备，资金年平均增长率可达到
．每年年底扣除下一年的消费基金后，余下的资金投入再生产．这家牛奶厂每年应扣除多少消费基金，才能实现经过５年资金达到2000万元的目标？
某人买了一辆价值
万元的新车，专家预测这种车每年按
的速度折旧．
（１）用一个式子表示
年后这辆车的价值．
（２）如果他打算用满４年时卖掉这辆车，他大概能得到多少钱？
某商场今年销售计算机5000台．如果平均每年的销售量比上一年的销售量增加
，那么从今年起大约几年可使总销售量达到30000台（结果保留到个位）？
试问:
与
(a、b＜0)的大小关系，并说明理由.
已知不等式(m2+4m－5)x2－4(m－1)x+3>0对一切实数x恒成立,求实数m的取值范围.