某营养师要为某个儿童预订午餐和晚餐,已知一个单位的午餐含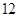 个单位的碳水化合物,
个单位的碳水化合物,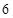 个单位的蛋白质和
个单位的蛋白质和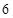 个单位的维生素
个单位的维生素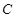 ;一个单位的晚餐含
;一个单位的晚餐含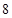 个单位的碳水化合物,
个单位的碳水化合物,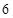 个单位的蛋白质和
个单位的蛋白质和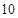 个单位的维生素
个单位的维生素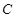 .另外,该儿童这两餐需要的营养中至少含
.另外,该儿童这两餐需要的营养中至少含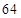 个单位的碳水化合物,
个单位的碳水化合物,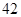 个单位的蛋白质和
个单位的蛋白质和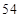 个单位的维生素
个单位的维生素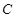 .如果一个单位的午餐、晚餐的费用分别是
.如果一个单位的午餐、晚餐的费用分别是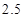 元和
元和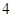 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
设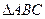 的内角
的内角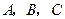 所对的边长分别为
所对的边长分别为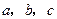 ,已知
,已知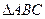 的周长为
的周长为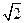 +1,且
+1,且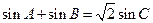 .
.
(1)求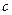 的值;
的值;
(2)若△ABC的面积为sinC,求角C的度数.
已知函数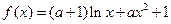 .
.
(Ⅰ)若函数 的最大值为1,求实数
的最大值为1,求实数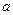 的值;
的值;
(Ⅱ)设 ,证明:对任意
,证明:对任意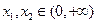 ,
,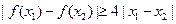 .
.
已知圆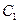 的方程为
的方程为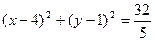 ,椭圆
,椭圆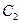 的方程
的方程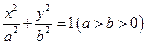 ,且离心率为
,且离心率为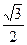 ,如果
,如果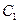 与
与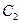 相交于
相交于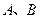 两点,且线段
两点,且线段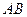 恰为圆
恰为圆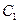 的直径.
的直径.
(Ⅰ)求直线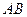 的方程和椭圆
的方程和椭圆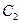 的方程;
的方程;
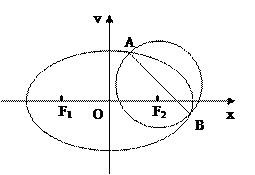
(Ⅱ)如果椭圆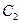 的左、右焦点分别是
的左、右焦点分别是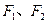 ,椭圆上是否存在点
,椭圆上是否存在点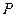 ,使得
,使得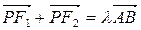 ,如果存在,请求点
,如果存在,请求点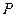 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
已知数列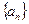 中,
中,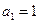 且
且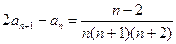 .
.
(I)设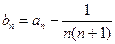 ,求数列
,求数列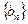 的通项公式;
的通项公式;
(II)设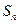 为数列
为数列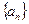 的前
的前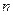 项和,求证:
项和,求证: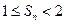 .
.
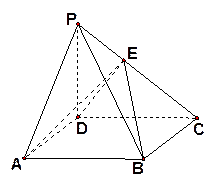
如图,四棱锥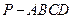 中,底面
中,底面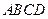 是平行四边形,
是平行四边形,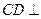 侧面
侧面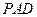 ,点
,点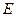 在侧棱
在侧棱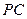 上,且
上,且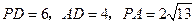 .
.
(Ⅰ)求证:平面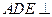 平面
平面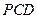 ;
;
(Ⅱ) 若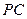 与
与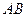 所成角为
所成角为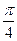 ,二面角
,二面角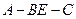 的大小为
的大小为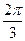 ,求
,求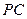 与平面
与平面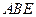 所成角的大小.
所成角的大小.