(本小题满分6分)已知函数 ,
,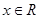
(1)求y取最大值时相应的x的集合;
(2)该函数的图象经过怎样的平移和伸缩变换可以得到函数y=sin x(x∈R)的图象.
在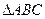 中,角A,B,C的对边分别为a,b,c,且满足
中,角A,B,C的对边分别为a,b,c,且满足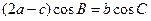
(1)求角B的大小;
(2)设向量 ,求
,求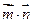 的最大值.
的最大值.
若曲线C: ,过
,过 上一点
上一点 作一斜率为
作一斜率为 的直线交曲线C于另一点
的直线交曲线C于另一点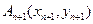 ,点
,点 的横坐标构成数列
的横坐标构成数列 ,其中
,其中 .
.
(1)求 与
与 的关系式;
的关系式;
(2)若 ,
,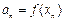 ,求
,求 的通项公式;
的通项公式;
(3)求证: .
.
(本小题满分13分)双曲线的中心是原点O,它的虚轴长为 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
(1)求双曲线的方程;
(2)若 =0,求直线PQ的方程.
=0,求直线PQ的方程.
(本小题满分12分)已知函数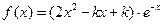 .
.
(1)当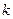 为何值时,
为何值时,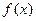 无极值;
无极值;
(2)试确定实数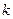 的值,使
的值,使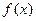 的极小值为
的极小值为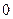 .
.
如图,三棱锥P—ABC中,PC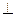 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD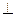 平面PAB.
平面PAB.
(1)求证:AB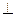 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求平面PAC和平面PAB所成锐二面角的余弦值.