如图,已知点 是离心率为
是离心率为 的椭圆
的椭圆 :
:
 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 ,
,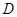 两点,且
两点,且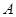 、
、 、
、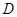 三点互不重合.
三点互不重合.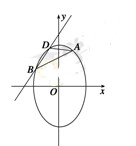
(1)求椭圆 的方程;(2)求证:直线
的方程;(2)求证:直线 ,
, 的斜率之和为定值.
的斜率之和为定值.
如图,已知四棱锥 ,底面
,底面 是等腰梯形,且
是等腰梯形,且 ∥
∥ ,
, 是
是 中点,
中点, 平面
平面 ,
, ,
,  是
是 中点.
中点.
(1)证明:平面 平面
平面 ;(2)求点
;(2)求点 到平面
到平面 的距离.
的距离.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.
(1)求 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取 个元件,元件寿命落在
个元件,元件寿命落在 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在 之间,一个元件寿命落在
之间,一个元件寿命落在 之间”的概率.
之间”的概率.
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列
,数列 的首项
的首项 ,
, .
.
(1)求函数 的表达式;(2)求数列
的表达式;(2)求数列 的前
的前 项和
项和 .
.
设函数 .
.
(1)若不等式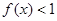 的解集为
的解集为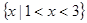 ,求
,求 的值;
的值;
(2)若存在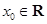 ,使
,使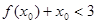 ,求
,求 的取值范围.
的取值范围.