商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加件,每件商品盈利元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
如图, 是平行四边形
是平行四边形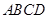 的对角线
的对角线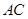 上的点,
上的点,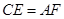 ,请你猜想:线段
,请你猜想:线段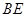 与线段
与线段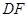 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。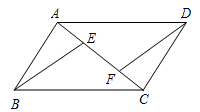
如图:两个同心圆的半径所截得的弧长AB=6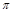 cm,CD=10
cm,CD=10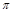 cm,且AC=12cm。(1)求两圆的半径长。(2)阴影部分的面积是多少?
cm,且AC=12cm。(1)求两圆的半径长。(2)阴影部分的面积是多少? 
如图,在由边长为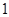 的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.
的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.
(1)请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上;
(2)在方格纸中将△A1B1C1经过怎样的变换后可以与△A2B2C2成中心对称图形?画出变换后的三角形并标出对称中心.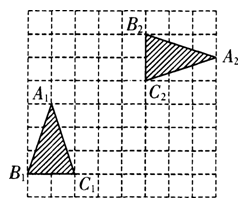
解方程: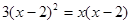 (因式分解)
(因式分解)