为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 |
北京 |
上海 |
天津 |
广州 |
| 人数 |
4 |
6 |
3 |
5 |
(1)从这18名对员中随机选出两名,求两人来自同一个队的概率;
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为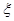 ,求随机变量
,求随机变量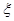 的分布列,及数学期望.
的分布列,及数学期望.
如图,三角形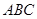 中,
中,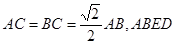 是边长为1的正方形,平面
是边长为1的正方形,平面 底面
底面 ,若
,若 分别是
分别是 的中点.
的中点.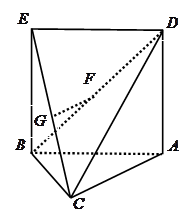
(1)求证: 底面
底面 ;
;
(2)求证: ⊥平面
⊥平面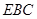 ;
;
(3)求几何体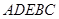 的体积
的体积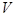 .
.
 某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
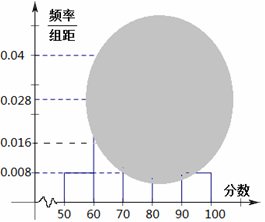
(1)求全班人数;
(2)求分数在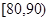 之间的人数;并计算频率分布直方图中
之间的人数;并计算频率分布直方图中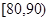 间的矩形的高;
间的矩形的高;
(3)若要从分数在 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在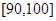 之间的概率.
之间的概率.
设函数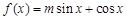
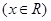 的图象经过点
的图象经过点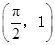 ,
,
(1)求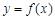 的解析式,并求函数的最小正周期和最大值;
的解析式,并求函数的最小正周期和最大值;
(2)如何由函数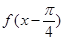 的图象得到函数
的图象得到函数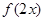 的图象.
的图象.
(本小题满分12分)设数列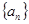 的前
的前 项和为
项和为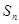 ,已知
,已知 ,
,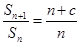 (
(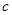 为常数,
为常数,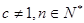 ),且
),且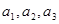 成等差数列.
成等差数列.
(1) 求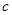 的值;
的值;
(2) 求数列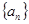 的通项公式;
的通项公式;
(3) 若数列 是首项为1,公比为
是首项为1,公比为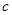 的等比数列,记
的等比数列,记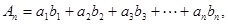
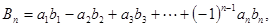
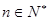
.求证: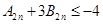 ,(
,(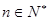 ).
).
(本小题满分10分)设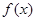
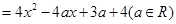 ,若方程
,若方程 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于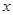 的不等式
的不等式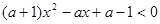 是否对一切实数
是否对一切实数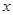 都成立?并说明理由。
都成立?并说明理由。