如图,三角形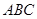 中,
中,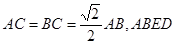 是边长为1的正方形,平面
是边长为1的正方形,平面 底面
底面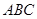 ,若
,若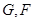 分别是
分别是 的中点.
的中点.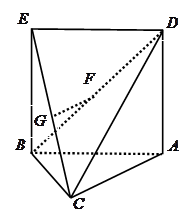
(1)求证: 底面
底面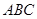 ;
;
(2)求证: ⊥平面
⊥平面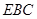 ;
;
(3)求几何体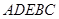 的体积
的体积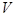 .
.
已知函数 ,
,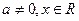 .
.
(I)讨论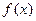 的单调性.
的单调性.
(II)当 时,讨论关于
时,讨论关于 的方程
的方程 的实根的个数.
的实根的个数.
如图某海滨城市为圆形区域,半径为 ,中心有某文化遗迹
,中心有某文化遗迹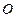 ,在该城市附近的海面上正在形成台风,据气象部门监测,目前台风中心位于文化遗迹
,在该城市附近的海面上正在形成台风,据气象部门监测,目前台风中心位于文化遗迹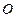 的南偏东
的南偏东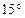 方向
方向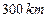 的海面
的海面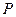 处,并以
处,并以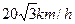 的速度向北偏西
的速度向北偏西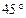 方向移动.如果台风侵袭的范围为圆形区域,且观测完成时,它正在形成,并它将以
方向移动.如果台风侵袭的范围为圆形区域,且观测完成时,它正在形成,并它将以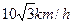 的速度不断增大.
的速度不断增大.
(I)该文化遗迹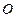 ,是否会受到台风的侵袭.如果会受到侵袭,会在几小时后?
,是否会受到台风的侵袭.如果会受到侵袭,会在几小时后?
(II)在几小时后,该城市开始受到台风侵袭,会历经多长时间?
已知函数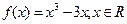 ,又
,又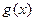 由
由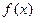 向右平移1个单位,向上平移2个单位得到.
向右平移1个单位,向上平移2个单位得到.
(I)判断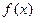 的奇偶性,并求出
的奇偶性,并求出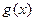 的极大值与极小值之和.
的极大值与极小值之和.
(II)过点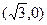 且方向向量为
且方向向量为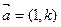 的直线与
的直线与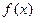 的图像相切,求实数
的图像相切,求实数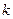 的值.
的值.
已知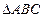 的周长为
的周长为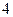 ,且
,且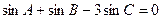 .
.
(I)求边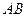 的长.
的长.
(II)若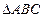 的面积恰为
的面积恰为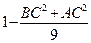 ,①求
,①求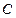 的正弦值. ②求
的正弦值. ②求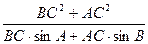 的值.
的值.
正方体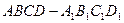 棱长为1,以
棱长为1,以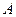 为坐标原点,以直线
为坐标原点,以直线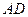 为横轴,直线
为横轴,直线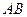 为纵轴,直线
为纵轴,直线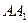 为竖轴建立空间直角坐标系,如图.
为竖轴建立空间直角坐标系,如图. 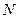 为
为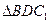 的重心,
的重心,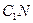
 于
于 .(I)求点
.(I)求点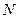 的坐标.(II)求直线
的坐标.(II)求直线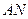 与平面
与平面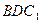 所成的角的大小.
所成的角的大小.