已知等差数列{an}是递增数列，且满足a4·a7＝15，a3＋a8＝8.
(1)求数列{an}的通项公式；
(2)令bn＝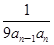
(n≥2)，b1＝
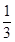，求数列{bn}的前n项和Sn.
已知数列{an}的前n项和为Sn，对一切正整数n，点Pn(n，Sn)都在函数f(x)＝x2＋2x的图象上，且在点Pn(n，Sn)处的切线的斜率为kn.
(1)求数列{an}的通项公式；
(2)若bn＝2knan，求数列{bn}的前n项和Tn.
已知数列an＝
求a1＋a2＋a3＋a4＋…＋a99＋a100的值．
已知等差数列{an}前三项之和为－3，前三项积为8.
(1)求等差数列{an}的通项公式；
(2)若a2，a3，a1成等比数列，求数列{|an|}的前n项和．
已知数列{an}的前n项和为Sn＝3n－1.
(1)求数列{an}的通项公式；
(2)若bn＝
(Sn＋1)，求数列{bnan}的前n项和Tn.
，若方程
有两个均小于2的不同的实数根，则此时关于
的不等式
是否对一切实数