(本小题满分12分)设数列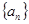 的前
的前 项和为
项和为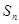 ,已知
,已知 ,
,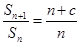 (
(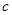 为常数,
为常数,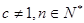 ),且
),且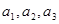 成等差数列.
成等差数列.
(1) 求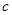 的值;
的值;
(2) 求数列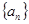 的通项公式;
的通项公式;
(3) 若数列 是首项为1,公比为
是首项为1,公比为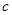 的等比数列,记
的等比数列,记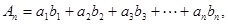
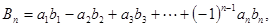
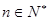
.求证: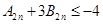 ,(
,(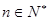 ).
).
已知平面向量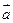
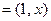 ,
,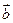

 .
.
(Ⅰ)若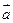 ⊥
⊥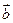 ,求x的值;
,求x的值;
(Ⅱ)若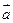 ∥
∥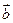 ,求|
,求|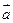 -
-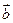 |.
|.
已知函数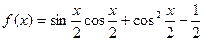 .
.
(Ⅰ)若 ;
;
(Ⅱ)求函数 在
在 上最大值和最小值.
上最大值和最小值.
设函数f(x)=xn(n≥2,n∈N*)
(1)若Fn(x)=f(x-a)+f(b-x)(0<a<x<b),求Fn(x)的取值范围;
(2)若Fn(x)=f(x-b)-f(x-a),对任意n≥a (2≥a>b>0),
证明:F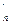 (n)≥n(a-b)(n-b)n-2。
(n)≥n(a-b)(n-b)n-2。
已知,A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于EF两点,交抛物线于M.N两点,交y轴于B.C两点
(1)当A点坐标为(8,4)时,求直线EF的方程;
(2)当A点坐标为(2,2)时,求直线MN的方程;
(3)当A点的横坐标大于2时,求△ABC面积的最小值。
设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若Sn=20,S2n=40,求S3n的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式SpSq<S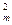 成立;
成立;
(3)是否存在常数k和等差数列{an},使ka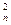 -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。