现在市面上有普通型汽车(以汽油为燃料)和电动型汽车两种。某品牌普通型汽车车价为12万元,第一年汽油的消费为6000元,随着汽油价格的不断上升,汽油的消费每年以20%的速度增长。其它费用(保险及维修费用等)第一年为5000元,以后每年递增2000元。而电动汽车由于节能环保,越来越受到社会认可。某品牌电动车在某市上市,车价为25万元,购买时一次性享受国家补贴价6万元和该市市政府补贴价4万元。电动汽车动力不靠燃油,而靠电池。电动车使用的普通锂电池平均使用寿命大约两年(也即两年需更换电池一次),电池价格为1万元,电动汽车的其它费用每年约为5000元。
求使用 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费 (万元)的表达式
(万元)的表达式
(总耗资费=车价+汽油费+其它费用)
比较两种汽车各使用10年的总耗资费用
(参考数据:

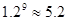
 )
)
选修4-5:不等式选讲
已知函数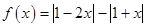
(1)解不等式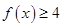 ;
;
(2)若函数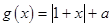 的图象恒在函数
的图象恒在函数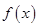 的图象的上方,求实数
的图象的上方,求实数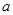 的取值范围.
的取值范围.
选修4-4:极坐标与参数方程
在极坐标系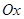 中,直线
中,直线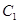 的极坐标方程为
的极坐标方程为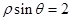 ,
,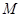 是
是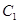 上任意一点,点
上任意一点,点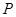 在射线
在射线 上,且满足
上,且满足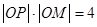 ,记点
,记点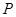 的轨迹为
的轨迹为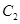 .
.
(1)求曲线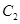 的极坐标方程;
的极坐标方程;
(2)求曲线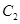 上的点到直线
上的点到直线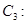
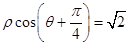 的距离的最大值.
的距离的最大值.
已知函数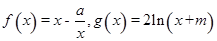 .
.
(1)当 ,存在
,存在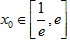 (
(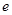 为自然对数的底数),使
为自然对数的底数),使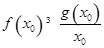 ,求实数
,求实数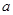 的取值范围;
的取值范围;
(2)当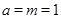 时,设
时,设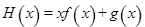 ,在
,在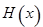 的图象上是否存在不同的两点
的图象上是否存在不同的两点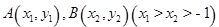 ,使得
,使得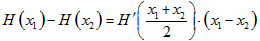 ?请说明理由.
?请说明理由.
已知抛物线 与圆
与圆 的两个交点之间的距离为4.
的两个交点之间的距离为4.
(1)求 的值;
的值;
(2)设过抛物线 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,与圆
两点,与圆 交于
交于 两点,当
两点,当 时,求
时,求 的取值范围.
的取值范围.
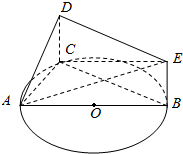
如图,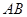 是圆
是圆 的直径,
的直径, 是圆
是圆 上异于
上异于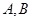 的一个动点,
的一个动点,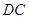 垂直于圆
垂直于圆 所在的平面,
所在的平面,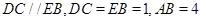 .
.
(1)求证: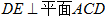 ;
;
(2)若 ,求平面
,求平面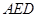 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.