选修4-4:极坐标与参数方程
在极坐标系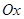 中,直线
中,直线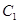 的极坐标方程为
的极坐标方程为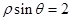 ,
,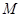 是
是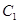 上任意一点,点
上任意一点,点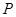 在射线
在射线 上,且满足
上,且满足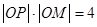 ,记点
,记点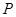 的轨迹为
的轨迹为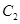 .
.
(1)求曲线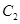 的极坐标方程;
的极坐标方程;
(2)求曲线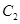 上的点到直线
上的点到直线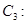
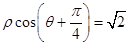 的距离的最大值.
的距离的最大值.
(本小题满分12分)已知函数 .
.
(1)判断 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断 在
在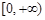 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(3)求满足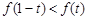 的
的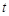 的取值范围.
的取值范围.
(本小题满分12分)某滨海高档住宅小区给每一户业主均提供两套供水方案.方案一是供应市政自来水,每吨自来水的水费是2元;方案二是限量供应10吨海底岩层中的温泉水,若温泉水用水量不超过5吨,则按基本价每吨8元收取,超过5吨不超过8吨的部分按基本价的1.5倍收取,超过8吨不超过10吨的部分按基本价的2倍收取.
(1)试写出温泉水用水费 (元)与其用水量
(元)与其用水量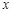 (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)若业主小王缴纳10月份的物业费时发现一共用水16吨,被收取的费用为72元,那么他当月的自来水与温泉水用水量各为多少吨?
(本小题满分12分)已知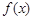 是定义在
是定义在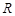 上的偶函数,且当
上的偶函数,且当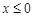 时,
时,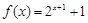 .
.
(1)求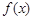 的解析式;
的解析式;
(2)在所给的坐标系内画出函数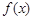 的草图,并求方程
的草图,并求方程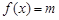 恰有两个不同实根时的实数
恰有两个不同实根时的实数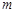 的取值范围.
的取值范围.
(本小题满分12分)已知全集为 ,集合
,集合 ,
,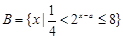 .
.
(1)当 时,求
时,求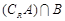 ;
;
(2)若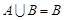 ,求实数
,求实数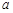 的取值范围.
的取值范围.
(本小题满分10分)计算下列各式:
(1)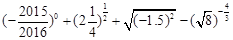 ;
;
(2)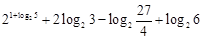 .
.