（本小题满分12分）某滨海高档住宅小区给每一户业主均提供两套供水方案．方案一是供应市政自来水，每吨自来水的水费是2元；方案二是限量供应10吨海底岩层中的温泉水，若温泉水用水量不超过5吨，则按基本价每吨8元收取，超过5吨不超过8吨的部分按基本价的1．5倍收取，超过8吨不超过10吨的部分按基本价的2倍收取．
（1）试写出温泉水用水费
（元）与其用水量
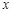（吨）之间的函数关系式；
（2）若业主小王缴纳10月份的物业费时发现一共用水16吨，被收取的费用为72元，那么他当月的自来水与温泉水用水量各为多少吨？
中，
，
，
，设E为
的中点，F为
的中点，在给定的空间直角坐标系D－xyz下，试写出A，B，C，D，
，
，
，
，E，F各点的坐标．
平面内的直线
上确定一点
；使
的距离最小．
，
，0），点D在平面yoz上，且
BDC=900，