已知数列{an}的前n项和为Sn，且满足an＝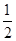
Sn＋1（n∈N*）；
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若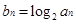
，cn＝
，且{cn}的前n项和为Tn，求使得
对n∈N*都成立的所有正整数k的值.
已知圆
的圆心在坐标原点O，且恰好与直线
相切.
(1)求圆的标准方程；
(2)设点A为圆上一动点，AN
轴于N，若动点Q满足
（其中m为非零常数），试求动点
的轨迹方程
.
(3)在（2）的结论下，当
时，得到动点Q的轨迹曲线C，与
垂直的直线
与曲线C交于 B、D两点，求
面积的最大值.
在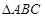
中，角A、B、C的对边分别为a、b、c，S是该三角形的面积
(1)若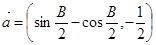
，
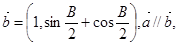求角B的度数
(2)若a=8，B=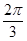
，S=
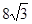，求b的值
(1)解方程：
(2)已知命题
命题
且命题
是
的必要条件，求实数m的取值范围
我们把离心率为e＝的双曲线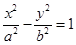
(a>0，b>0)称为黄金双曲线．如图，
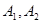是双曲线的实轴顶点，
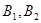是虚轴的顶点，
是左右焦点，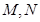
在双曲线上且过右焦点
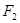，并且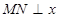
轴，给出以下几个说法：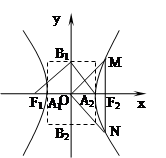
①双曲线x2－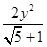
＝1是黄金双曲线；
②若b2＝ac，则该双曲线是黄金双曲线；
③如图，若∠F1B1A2＝90°，则该双曲线是黄金双曲线；
④如图，若∠MON＝90°，则该双曲线是黄金双曲线．
其中正确的是( )
| A．①②④ | B．①②③ | C．②③④ | D．①②③④ |
已知椭圆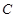
的中心在坐标原点，焦点在
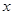轴上且过点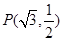
，离心率是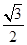
．
（1）求椭圆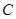
的标准方程；
（2）直线过点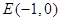
且与椭圆交于
，
两点，若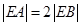
，求直线的方程.