已知函数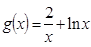
，
，
．
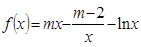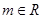（1）求函数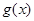
的极值点；
（2）若
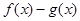在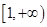
上为单调函数，求
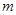的取值范围；
（3）设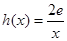
，若在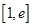
上至少存在一个
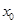，使得
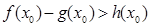成立，求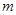的取值范围．
(本小题满分13分)
设椭圆
的离心率
，右焦点到直线
的距离
为坐标原点.
（I）求椭圆
的方程；
（II）过点作两条互相垂直的射线，与椭圆分别交于
两点，证明点到直
线
的距离为定值，并求弦长度的最小值.
(本小题满分13分)
质点在
轴上从原点
出发向右运动，每次平移一个单位或两个单位，且移动一个单位的概率为
，移动2个单位的概率为
，设质点运动到点
的概率为
.
（Ⅰ）求
和
；
（Ⅱ）用
表示，并证明
是等比数列；
（Ⅲ）求.
(本小题满分13分)
如图，矩形ABCD和梯形BEFC所在平面互相垂直，BE∥CF且BE＜CF,∠BCF=
，AD=
，EF=2.
（Ⅰ）求证： AE∥平面DCF；
（Ⅱ）若
，且二面角A—EF—C的大小为
，求
的长。
(本小题满分13分)
已知
，
，函数
，
（Ⅰ）求
时，函数
的取值范围；
（Ⅱ）在
中，a、b、c分别是角A、B、C、的对边，且
，
，求
的面积.
双曲线M的中心在原点，并以椭圆
的焦点为焦点，以抛物线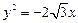
的准线为右准线.
（1）求双曲线M的方程；
（2）设直线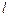
：
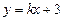与双曲线M相交于A、B两点，O是原点.
① 当
为何值时，使得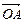
?
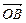
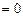② 是否存在这样的实数,使A、B两点关于直线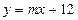
对称？若存在，求出的值；若不存在，说明理由.