已知函数y与x+1成反比例,且当x=﹣2时,y=﹣3.
(1)求y与x的函数关系式;
(2)当x= 时,求y的值.
时,求y的值.
解方程:
① ;
;
②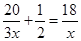 ;
;
③ ;
;
④ .
.
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E.
(1)若PB平分∠ABO,求证:AP=CD;
(2)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
小明和小新同时上学,从家到学校的距离都是2km,他们走路的速度是6km/h,跑步的速度为10km/h,请你根据以上信息,设计一个可以用一元一次不等式解决的问题.并给出解决方案.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
(1)求证:点D在AB的中垂线上;
(2)如果△ACD的面积为1,求△ADB的面积.