提出问题
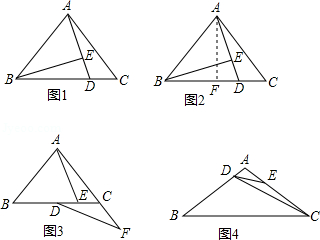
如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
类比探究
如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
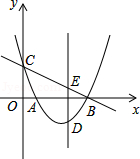
如图,在平面直角坐标系 中,抛物线 与 轴相交于点 ,点 与点 关于点 对称
(1)填空:点 的坐标是 ;
(2)过点 的直线 (其中 与 轴相交于点 ,过点 作直线 平行于 轴, 是直线 上一点,且 ,求线段 的长(用含 的式子表示),并判断点 是否在抛物线上,说明理由;
(3)在(2)的条件下,若点 关于直线 的对称点 恰好落在该抛物线的对称轴上,求此时点 的坐标.
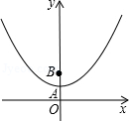
阅读下面材料:
小明遇到这样一个问题:如图1, 中, ,点 在 边上, , ,垂足为 ,求证: .
小明经探究发现,过点 作 ,垂足为 ,得到 ,从而可证 (如图 ,使问题得到解决.
(1)根据阅读材料回答: 与 全等的条件是 (填“ ”、“ ”、“ ”、“ ”或“ ”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3, 中, , , 为 的中点, 为 的中点,点 在 的延长线上,且 ,若 ,求 的长;
(3)如图4, 中, , ,点 、 分别在 、 边上,且 (其中 , ,求 的值(用含 的式子表示).
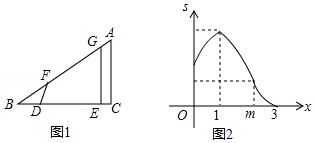
如图1, 中, ,线段 在射线 上,且 ,线段 沿射线 运动,开始时,点 与点 重合,点 到达点 时运动停止,过点 作 ,与射线 相交于点 ,过点 作 的垂线,与射线 相交于点 .设 ,四边形 与 重叠部分的面积为 , 关于 的函数图象如图2所示(其中 , , 时,函数的解析式不同)
(1)填空: 的长是 ;
(2)求 关于 的函数关系式,并写出 的取值范围.
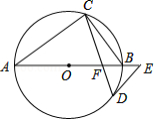
如图, 是 的直径,点 、 在 上, ,点 在 的延长线上, .
(1)求证: 与 相切;
(2)若 , ,求 的半径.
如图,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,点 是直线 下方抛物线上一点,过点 作 轴的平行线,与直线 相交于点
(1)求直线 的解析式;
(2)当线段 的长度最大时,求点 的坐标.